Teorema dell'esistenza e dimostrazione di unicità, esempi ed esercizi

Lui Teorema di esistenza e unicità stabilisce le condizioni necessarie e sufficienti per un'equazione differenziale di primo ordine, con una data condizione iniziale, per avere una soluzione e che questa soluzione è anche l'unica. 

Tuttavia, il teorema non fornisce alcuna tecnica o indicazione di come trovare una tale soluzione. L'esistenza e il teorema dell'unicità si estendono anche alle equazioni differenziali di ordine superiore con condizioni iniziali, che è noto come problema di Cauchy.

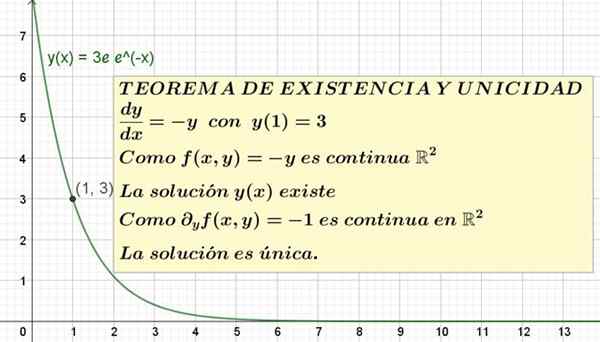
Figura 1. È mostrata un'equazione differenziale con la condizione iniziale e la sua soluzione. L'esistenza e il teorema dell'unicità garantiscono che è l'unica soluzione possibile.

La dichiarazione formale dell'esistenza e del teorema di unicità è la seguente:

"Per un'equazione differenziale e '(x) = f (x, y) con condizione iniziale e (a) = b,  esiste almeno una soluzione in una regione rettangolare del piano XY contenente il punto (A, b), Sì f (x, y) È continuo in quella regione. E se il derivato parziale di F nel rispetto di E: G = ∂f/ ∂y È continuo nella stessa regione rettangolare, quindi la soluzione è unica in un ambiente del punto (A, b) contenuto nella regione di continuità di F E G."

L'utilità di questo teorema sta prima per sapere quali sono le regioni del piano XY in cui può esserci una soluzione e sapere anche se la soluzione trovata è l'unica possibile o se ce ne sono altri. 

Si noti che nel caso in cui la condizione di unica.

[TOC]

Dimostrazione dell'esistenza e del teorema di unicità

figura 2. A Charles Émile Picard (1856-1941) Una delle prime dimostrazioni dell'esistenza e del teorema dell'unicità è accreditata. Fonte: Wikimedia Commons.

Per questo teorema, sono note due possibili dimostrazioni, una di queste è la dimostrazione di Charles Émile Picard (1856-1941) e l'altra è dovuta a Giuseppe Peano (1858-1932) in base alle opere di Augustin Louis Cauchy (1789-1857 ).

Può servirti: vettori simultanei: caratteristiche, esempi ed esercizi

Va notato che le menti matematiche più brillanti del diciannovesimo secolo hanno partecipato alla dimostrazione di questo teorema, quindi può essere intuitiva che nessuno dei due è semplice.

Per dimostrare formalmente il teorema, è necessario prima stabilire una serie di concetti matematici più avanzati, come le funzioni di tipo Lipschitz, gli spazi di Banach, il carateo e molti altri teoremi di esistenza, che sfuggono allo scopo dell'articolo.

Gran parte delle equazioni differenziali che vengono gestite in fisica si occupano di funzioni continue nelle regioni di interesse, quindi ci limiteremo a mostrare il modo in cui il teorema viene applicato in equazioni semplici.

Esempi

- Esempio 1

Considera la seguente equazione differenziale con una condizione iniziale:

e '(x) = - y; con e (1) = 3

C'è una soluzione per questo problema? È l'unica soluzione possibile?

Risposte

In primo luogo, viene valutata l'esistenza della soluzione dell'equazione differenziale e che soddisfa anche la condizione iniziale. 

In questo esempio f (x, y) = - y La condizione dell'esistenza richiede di sapere se  f (x, y) È continuo in una regione aerea XY contenente il punto di coordinate x = 1, y = 3.

Ma f (x, y) = -y È il funzione correlata, che è continuo nel dominio di numeri reali ed esiste nell'intera gamma di numeri reali.

Pertanto si è concluso che f (x, y) è continuo in r², Quindi il teorema garantisce l'esistenza di almeno una soluzione.

Sapere questo, è tempo di valutare se la soluzione è unica o se al contrario ce n'è più di uno. Per questo è necessario calcolare il derivato parziale di F Per quanto riguarda la variabile E:

∂f/∂y = ∂ (-y)/∂y = -1

COSÌ G (x, y) = -1 che è una funzione costante, che è anche definita per tutti r² Ed è anche continuo lì. Ne consegue che l'esistenza e il teorema dell'unicità garantiscono che questo problema di valore iniziale abbia una soluzione unica, sebbene non ci dica cosa sia.

Può servirti: poligono convesso: definizione, elementi, proprietà, esempi

- Esempio 2

Prendi in considerazione la seguente equazione differenziale ordinaria del primo ordine con condizione iniziale:

e '(x) = 2√y; e (0) = 0.

C'è una soluzione e (x) Per questo problema? In tal caso, determina se ce n'è uno o più di uno.

Risposta

Consideriamo la funzione f (x, y) = 2√y. La funzione F è definito solo per Y≥0, Bene, sappiamo che un numero negativo manca di radice reale. Oltretutto f (x, y) È continuo nel semiplano superiore di R²  compreso l'asse x, così Le garanzie di esistenza e teorema di unicità Almeno una soluzione in quella regione.

Ora, la condizione iniziale x = 0, y = 0 è al bordo della regione della soluzione. Quindi prendiamo il derivato parziale di f (x, y) rispetto a y:

∂f/∂y = 1/√y

In questo caso la funzione non è definita per y = 0, proprio dove è la condizione iniziale.

Cosa ci dice il teorema? Ci dice che sebbene sappiamo che esiste almeno una soluzione il semiplano superiore dell'asse X incluso l'asse X, poiché la condizione di unicità non è soddisfatta, non vi è alcuna garanzia che esista una sola soluzione.

Ciò significa che potrebbe esserci una o più di una soluzione nella regione di continuità di F (x, y). E come sempre, il teorema non ci dice cosa potrebbe essere.

Esercizi risolti

- Esercizio 1

Risolvi il problema di Cauchy dell'esempio 1:

e '(x) = - y; con e (1) = 3. 

Trova la funzione y (x) che soddisfa l'equazione differenziale e la condizione iniziale.

Soluzione

Nell'esempio 1 è stato determinato che questo problema ha una soluzione ed è anche unico. Per trovare la soluzione, la prima cosa che si dovrebbe notare è che si tratta di un'equazione differenziale di primo grado di variabili separabili, che è scritta come segue:

Può servirti: coefficiente di variazione: a cosa serve, calcolo, esempi, esercizi

dy /dx = - e → dy = -y dx

Dividi tra e in entrambi i membri per separare le variabili che abbiamo:

dy/y = - dx

Viene applicato l'integrale indefinito in entrambi i membri:

∫ (1/y) dy = - ∫dx

Risolvere gli integrali indefiniti è:

ln (y) = -x + c

dove c è una costante di integrazione determinata dalla condizione iniziale:

ln (3) = -1 + c, vale a dire che c = 1 + ln (3)

Sostituire il valore di C e la riorganizzazione è:

ln (y) - ln (3) = -x + 1

Applicazione della seguente proprietà dei logaritmi:

La differenza nei logaritmi è il logaritmo del quoziente

L'espressione precedente può essere riscritta in questo modo:

ln (y/3) = 1 - x

La funzione esponenziale viene applicata con entrambi i membri per ottenere:

Y / 3 = e^{(1 - x)}

Che è equivalente a:

 y = 3e e^-X

Questa è la soluzione unica dell'equazione e '= -y con y (1) = 3. Il grafico di questa soluzione è mostrato nella Figura 1.

- Esercizio 2

Trova due soluzioni al problema sollevato nell'esempio 2:

e '(x) = 2√ (y); e (0) = 0.

Soluzione

È anche un'equazione di variabili separate, che è scritta in modo differenziato:

Dy / √ (y) = 2 dx

Rimane l'integrale indefinito in entrambi i membri:

2 √ (y) = 2 x + c

Come è noto Y≥0 Nella regione della soluzione che abbiamo:

y = (x + c)² 

Ma come deve essere soddisfatta la condizione iniziale x = 0, y = 0, la costante C è zero e rimane la seguente soluzione:

e (x) = x².

Ma questa soluzione non è unica, la funzione y (x) = 0 è anche una soluzione del problema sollevato. L'esistenza e il teorema di unicità applicato a questo problema nell'esempio 2 aveva già previsto che potesse esserci più di una soluzione.

Riferimenti

1. Coddington, Earl A.; Levinson, Norman (1955), Teoria delle equazioni differenziali ordinarie, New York: McGraw-Hill.
2. Enciclopedia della matematica. Teorema di Cauchy-Lipschitz. Recuperato da: enciclopediaofmath.org
3. Lindelöf, South L'Applicazione del Methode des a Approssimazioni successive Aux Équations Différentielles Ordinaires du Premier Ordre; Compttes Rendus Hebdomadaires des Séances de L'An Ac Acadequie des Sciences. Vol. 116, 1894, pp. 454-457. Recuperato da: gallico.Bnf.fr.
4. Wikipedia. Il metodo degli approcci successivi di Picard. Recuperato da: è.Wikipedia.com
5. Wikipedia. Teorema di Picard-Lindelöf. Recuperato da: è.Wikipedia.com.
6. Zill, d.1986. Equazioni differenziali elementari con applicazioni.Prentice Hall.